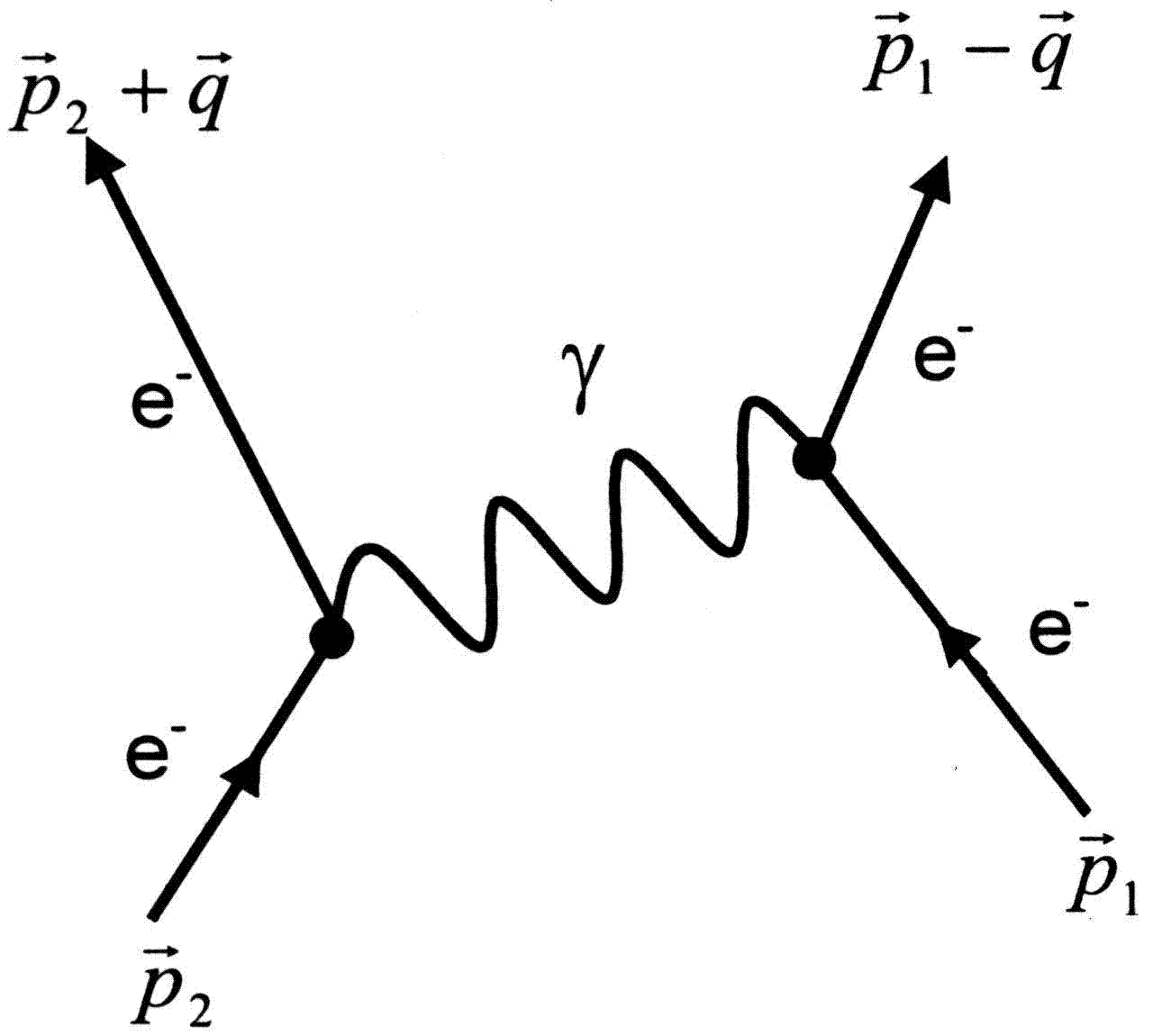
Die beiden eben dargestellten Feynman-Diagramme sind Diagramme erster Ordung, da sie nur einen Vertex haben. Aufgrund der Energie- und Impulserhaltung, die wie angemerkt in jedem Vertex gelten muss, können aber nicht alle hinein- und herauslaufenden Linien reellen Teilchenzuständen entsprechen. Diese Prozesse sind somit in der Natur nicht beobachtbar.
Kombiniert man zwei Diagramme erster Ordnung, so ergibt sich ein Diagramm zweiter Ordnung, also eines mit 2 Vertices.
Eine solche Wechselwirkung ist z.B. die Elektron-Elektron-Streuung, an der ein virtuelles Photon beteiligt ist.

Hier muss sich allerdings die Frage gestellt werden, ob man nicht auch auf andere Weise die gleichen Ergebnisse erhalten kann. Das würde bedeuten, dass es unendlich viele Möglichkeiten gäbe, ein Feynman-Diagramm aufzustellen. Dies ist auch der Fall. Auf die Auswirkung wird hier später eingegangen. Andere Diagramme wären z.B.:
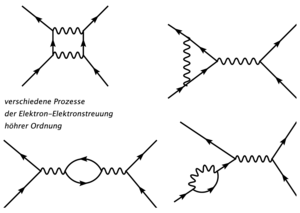
[Quelle: Wikipedia, Suchbegriff: Feynman-Diagramm, Stand: 20.08.2005]
Die Elektron-Photon-Streuung, auch Compton-Effekt genannt, wird als Feynman-Diagramm folgendermaßen dargestellt:
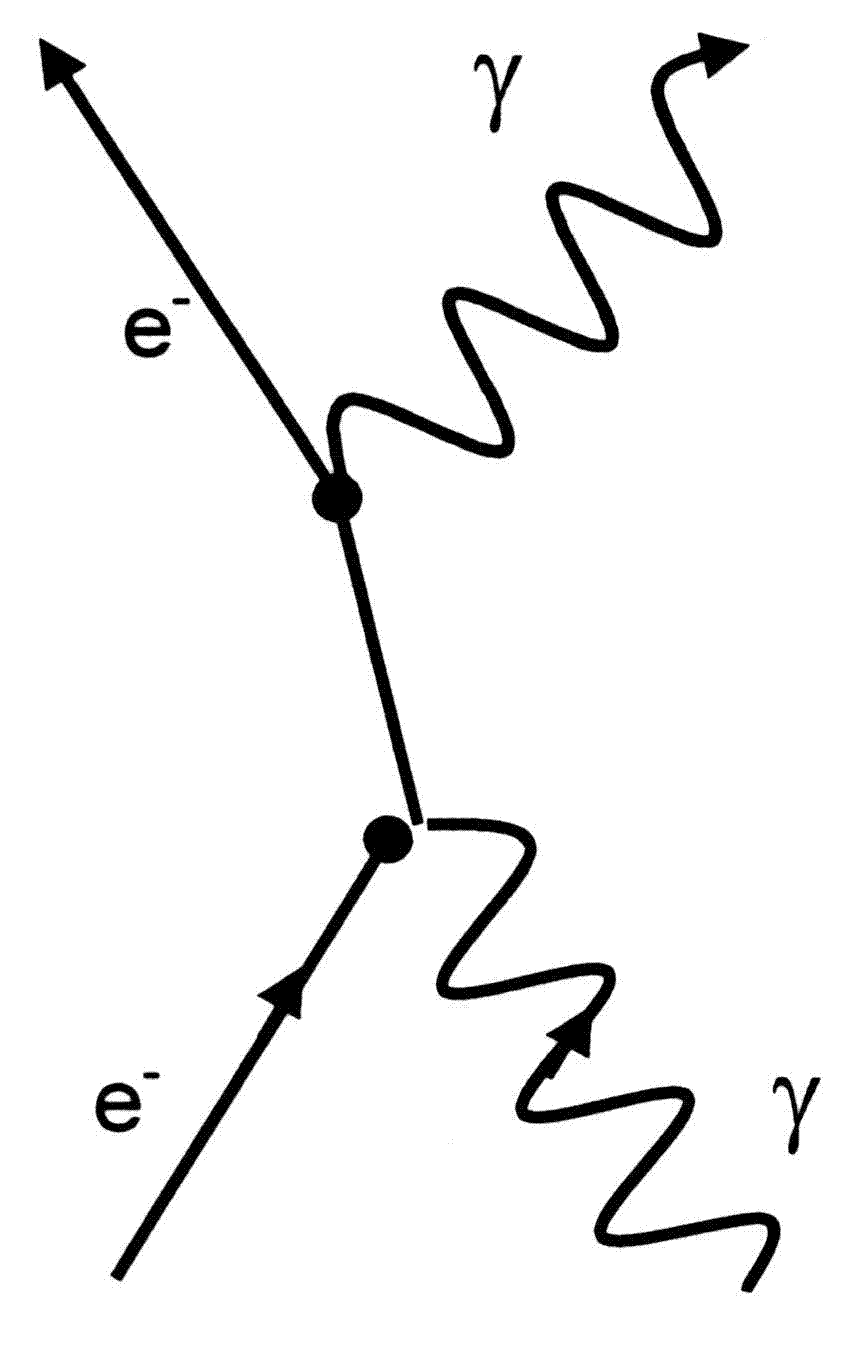
Neben den Prozessen zweiter Ordnung soll hier auch ein Prozess dritter Ordnung dargestellt werden. Die e−-e−-Bremsstrahlung:
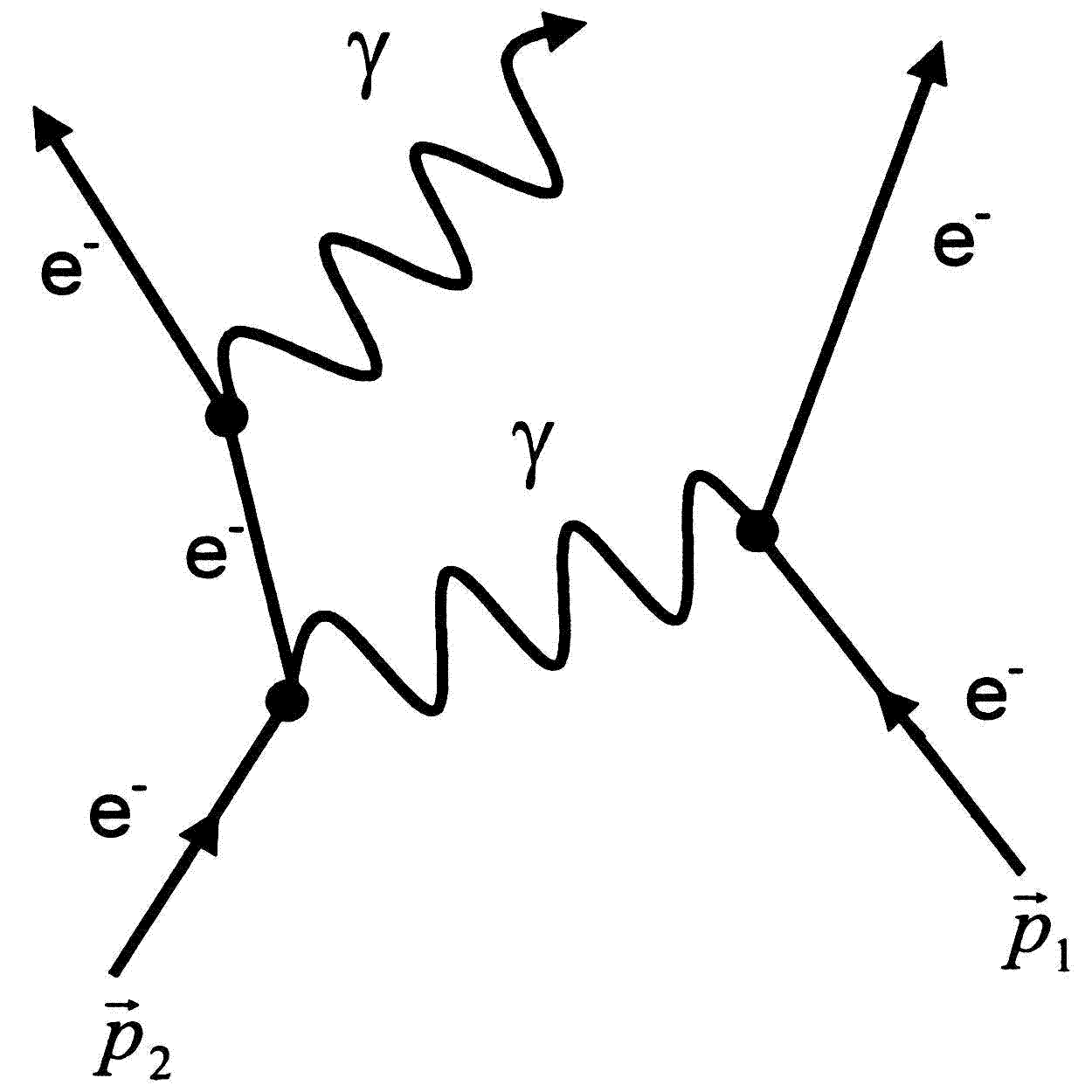
Wichtiger als die Möglichkeit aus Feynman-Diagrammen Operatoren abzulesen ist, dass man mit Hilfe der Feynman-Diagramme auch die Rechnungen für die Übergangsamplitude (sie
stellt die Wahrscheinlichkeit dar, dass der Prozess stattfindet) rückübersetzen kann. Hierbei kommen nun die verschiedenen Möglichkeiten zum Tragen.
Für die Berechnungen dieser Amplitude kommt das sog. Feynman-Kalkül zum Einsatz. Kurz gefasst besagt dies, dass alle Möglichkeiten zur Amplitude beitragen. Je mehr Vertices ein Diagramm enthält, desto geringer wird sein Beitrag zur Gesamtamplitude.
Die heute bekannten, überragend genauen Ergebnisse der Quantenelektrodynamik kommen zustande, indem man alle Prozesse bis zur vierten Ordnung einbezieht.