Die erzwungene, gedämpfte Drehschwingung

Bei der erzwungenen, gedämpften Drehschwingung wird dem System ein periodisches äußeres Drehmoment aufgeprägt. Die Bewegungsgleichung lautet dann:

oder:

 , mit  und  .

Als Lösung erhalten wir:

mit der Amplitude 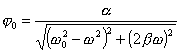   (1)

und einer Phase                       (2)

Aus den Beziehungen (1) und (2) ergeben sich Folgerungen für das Schwingungsverhalten der erzwungenen Schwingungen.

• Welches Verhältnis haben die Frequenzen des Erregers und des Resonators zueinander?
• Was sagt die Phasenkonstante über die Beziehung zwischen Erreger und Resonator aus?
• Wovon sind die Amplitude und die Phase abhängig?

Die Antworten auf diese Fragen finden sie hier.

Im Praktikumversuch sollen Sie unter anderem die Eigenfrequenz des Drehpendels bestimmen. Diese finden Sie wenn das Drehpendel in Resonanzschwingung gebracht wird, also wie bei linearen Schwingungen ist.

Aufgrund der Dämpfung ist allerdings die maximale Amplitude verschoben, also