Verlauf der Dampfdruckkurve

Betrachten wir den Phasenübergang von einer Phase A auf eine andere Phase B. Die Phase A habe zunächst das Volumen V_A . Nach der Umwandlung in die Phase B hat sich dieses auf V_B geändert. Ganz allgemein ist die Steigung der Koexistenzkurve p_k(T) beider Phasen im pT-Diagramm durch die Clausius-Clapeyronsche Gleichung gegeben:

Hierbei bezeichnet Q_L die molare latente Wärme des Phasenübergangs und n die Anzahl der betrachteten Mole des Stoffes. Da im allgemeinen V_B > V_A , ist die Steigung in der Regel positiv.

Beim Prozess des Verdampfens müssen wir die flüssige (Phase B) und die gasförmige Phase (Phase A) betrachten. Das Volumen der Gasphase V_B ist sehr viel größer als das der flüssigen Phase V_A, so dass wir näherungsweise

setzen können. Ferner können wir V_B (für hohe Temperaturen T) mit Hilfe der allgemeinen Gasgleichung ausdrücken:

Einsetzen liefert dann

bzw.

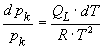
Integration mit der Randbedingung p_k(T₀ ) = p_k0 liefert:

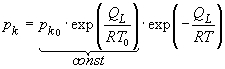
Da die ersten beiden Faktoren sind konstant sind, ist

.

Die Dampfdruckkurve p_k(T) steigt also mit der Temperatur T exponentiell an.