Eine bestimmte Menge Luft habe bei 20 °C bei einem
Druck von 1000 hPa ein Volumen von 2 Litern. Die Luftmenge (Adiabaten-Exponent
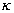= 1.4)
expandiere adiabatisch auf das doppelte Volumen. Berechnen Sie denn Enddruck
und vergleichen Sie diesen mit dem einer isothermen Expansion.
Für eine adiabatische Zustandsänderung lautet
die Zustandsgleichung:
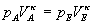
Hier bezeichnet der Index A den Anfangszustand und der Index E den Endzustand.
Diese Gleichung lösen wir nach pE auf
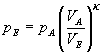
Nach Einsetzen der Werte erhalten wir
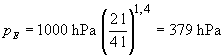
Für eine isotherme Zustandsänderung gilt:
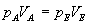
und damit
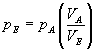
Einsetzen der Werte liefert
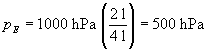
Der Enddruck bei der isothermen Zustandsänderung ist also deutlich größer
als bei der adiabatischen. Dies ist anschaulich klar, da der Luft bei der
isothermen Zustandsänderung Wärmeenergie aus der Umgebung zugeführt
werden muss. Diese zusätzliche Energie fehlt bei der adiabatischen Zustandsänderung,
die Temperatur und damit der Druck sinken.
Berechnen Sie für die vorherige Aufgabe die Endtemperatur
der eingeschlossenen Luftmenge.
Für eine adiabatische Zustandsänderung lautet die Beziehung zwischen
Volumen und Temperatur (vergleiche Herleitung der Poisson'schen Gleichung):
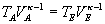
Diese Gleichung stellen wir nach TE um:
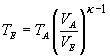
Wir setzen jetzt die gegebenen Werte ein und beachten, dass hier für
TA die absolute Temperatur einzusetzen (20 °C = 293 K) ist.
Wir erhalten dann:
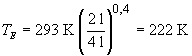
222 K entsprechen -51 °C. Die Temperatur ist also bei eine Verdoppelung
des Volumens deutlich um über 70 °C abgefallen!
